Introduction: Why VaR Matters
In financial markets, risk is just as important as return. Investors, traders, and regulators all want to know: What is the worst-case scenario if markets move against us?
This is where Value at Risk (VaR) comes in. VaR is often described as the “gold standard” of risk measurement because it condenses complex statistical analysis into a single number that represents potential loss.
From hedge funds managing billions to banks complying with Basel Accords, VaR plays a central role in risk management frameworks.
What Is Value at Risk (VaR)?
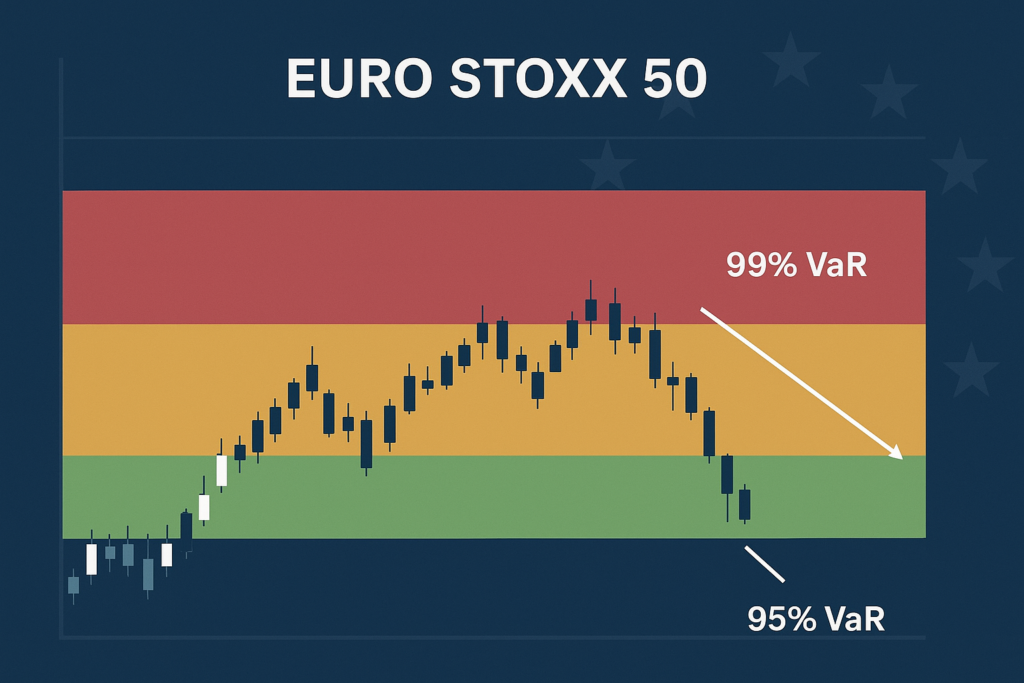
Value at Risk (VaR) estimates the maximum expected loss of an investment or portfolio within a defined time horizon, given a confidence level.
For example:
- A 1-day 95% VaR of $1 million means there is only a 5% chance the portfolio will lose more than $1 million in a single day.
Thus, VaR is built on three elements:
- Time Horizon – e.g., one day, one week, one month.
- Confidence Level – typically 95% or 99%.
- Loss Amount – expressed in absolute dollars or percentage terms.
Methods of Calculating VaR
1. Historical Method
- Uses past market data to simulate future returns.
- Simple and intuitive – assumes history repeats itself.
- Example: If 250 days of returns are ranked, the 5th-worst outcome reflects the 95% VaR.
2. Variance-Covariance (Parametric) Method
- Assumes returns follow a normal distribution.
- Requires mean (expected return) and standard deviation (volatility).
- Example:
- If daily volatility is 2%, then at 95% confidence (1.65σ), VaR = -3.3%.
3. Monte Carlo Simulation
- Uses random sampling to simulate thousands of possible price paths.
- Captures complex relationships and non-linear risks.
- Often used for large portfolios with derivatives.
Worked Example: Calculating VaR
Suppose a portfolio worth $10 million has a daily volatility of 1.5%.
- At 95% confidence (1.65σ): VaR = 10,000,000 × 1.65 × 0.015 = $247,500.
- Interpretation: There’s a 5% chance the portfolio could lose more than $247,500 in one day.
Advantages of VaR
- Simple and intuitive: One number to summarize risk.
- Universally accepted: Standardized across banks and institutions.
- Flexible: Can be applied to stocks, bonds, currencies, and derivatives.
Limitations of VaR
- Model risk: Different methods yield different results.
- Ignores extreme events (tail risk): Cannot predict “black swan” crashes.
- Portfolio complexity: Correlations make calculations harder for large portfolios.
- Backward-looking: Relies on historical data and assumptions.
Beyond Basic VaR: Variants and Extensions
- Marginal Value at Risk (MVaR) – Additional risk from adding a new investment.
- Incremental Value at Risk (IVaR) – Change in portfolio risk from buying/selling assets.
- Conditional Value at Risk (CVaR) – Expected loss beyond the VaR threshold, often considered more robust.
Applications of VaR
- Banks & Basel Accords: Regulators require banks to report VaR to ensure capital adequacy.
- Trading Desks: Daily VaR limits help traders manage exposure.
- Portfolio Managers: Used to balance risk-return tradeoffs.
- Risk Reporting: Provides investors and executives with a clear snapshot of downside risk.
VaR vs Conditional VaR (CVaR)
While VaR tells you the maximum expected loss within a confidence level, CVaR goes further by showing the average loss if VaR is breached.
- Example: If 95% VaR is $1M, CVaR might say the average loss in the worst 5% of cases is $1.5M.
Common FAQs About VaR
1. What does a high VaR mean?
It indicates a larger potential loss — higher risk exposure.
2. Is VaR always reliable?
No. It depends heavily on assumptions about return distributions and correlations.
3. Why is VaR important for banks?
It’s mandated by regulators (Basel framework) to ensure institutions hold enough capital to withstand losses.
4. Which VaR method is best?
There is no one-size-fits-all. Historical is simple, parametric is efficient, and Monte Carlo is flexible but computationally heavy.
The Bottom Line
Value at Risk (VaR) remains one of the most widely used measures of financial risk. While not perfect, it provides a standardized and practical way to estimate potential portfolio losses.